おみやげ算を初心者向けにわかりやすく図を使って解説します。
特別な計算方法になると身構えてしまいがちですが、とても簡単で小学生でも使えますよ。
おみやげ算とは?その計算方法をわかりやすく図解します。
おみやげ算とは?
おみやげ算とは、二桁の掛け算(かけ算)を筆算を使わずに暗算で計算する方法です。
隣りに数を移動させる動作が「おみやげ(お土産)」に似ていることが由来のようです。
(由来についてご存じの方は教えてもらえると嬉しいです。)
小学校の授業では習わずに筆算を使うのが基本になっていますが、簡単に使えることから最近書籍などで大人気。
早く計算する必要がある中学受験でも使われています。
10以上のかけ算はもちろんのこと、20以上、30以上のかけ算にも使えます。
ただし、一つだけ条件があります
おみやげ算の条件、できないものもある

おみやげ算は十の位が同じ数の時だけしか使えない、という条件があります。
上の図だと例題1は十の位が「2と2」なのでおみやげ算が使えますが、例題2は十の位が「1と2」、例題3は十の位が「3と1」と数が異なるのでできません。
例題を用意し計算した内容については「おみやげ算の条件とは?計算できないものがあるのはなぜ?」にまとめています。
実際に計算すると合わないことがわかります。必ず10の位が同じ数の時だけおみやげ算を使いましょう。
おみやげ算の計算方法をわかりやすく図解
以上のことを理解した上で、おみやげ算の解説をしていきます。
おみやげ算は大きく3つの計算をしますが、暗算できるのでそれほど難しくありません。
今回は「14×13」を例として、図解1〜3の順に解き方をまとめました。
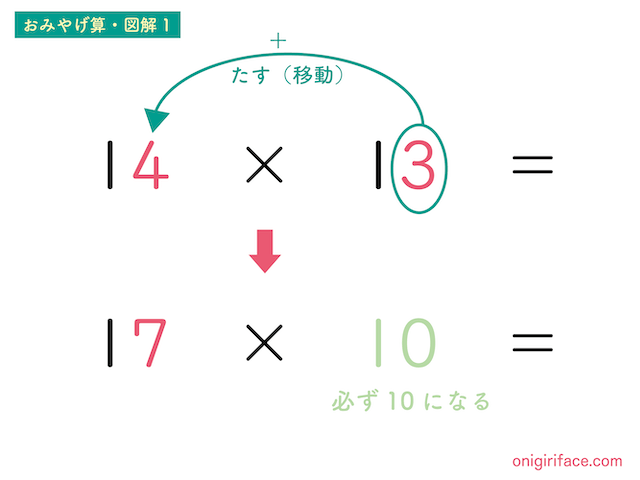
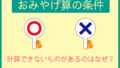
まずは図解1を見て下さい。「14×13」それぞれの一の位を見ます。
かける方の一の位は「3」に、かけられる方の一の位「4」に足します(左に移動するイメージ)。すると1つ目の数が「4+3=7」になりました。
後ろの一の位「3」が、前の一の位「4」に移動したことから、残りの数は10になります(図解1:13-3=10)。
移動させたあとは掛け算です。あとの数字が10になるので、最初の17に0をつけるだけ、答えは170になりますね。「170×10=170」
十の位が10の場合、後ろの数字が必ず「10」になるので計算しやすいのがポイントです。
※十の位が20の場合は「20」、十の位が30の場合は「30」になる。
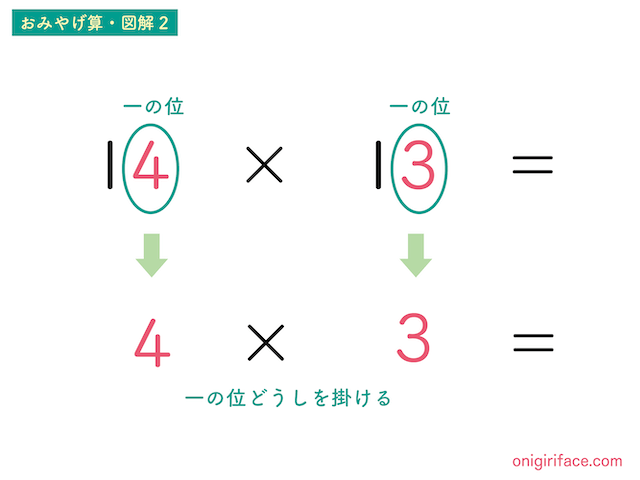
図解2に進みます。次は一の位どうしを掛け算します。
「14×13」の一の位どうしは「4×3」。九九で「4×3=12」になります。
図解2は簡単ですね。
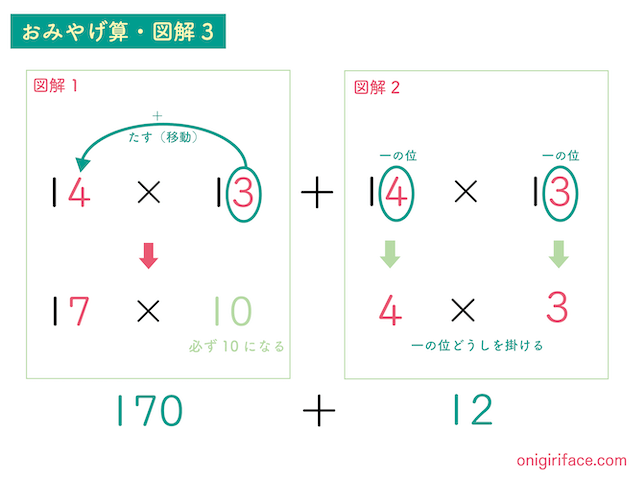
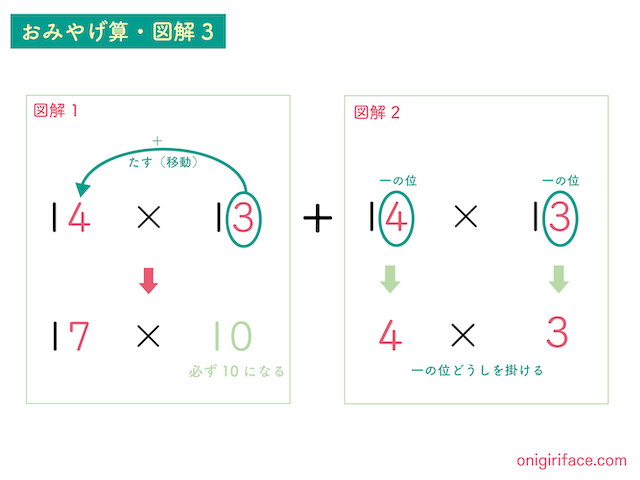
最後に図解3です。
これまで暗算でしてきた図解1と図解2を最後に足します。
- 図解1の計算:「14×13」→「17✕10=170」
- 図解2の計算:「4×3=12」
- 図解3の計算:「170+12=182」
最後に図解1の170と図解2の12を足すので182となりました。
以上がおみやげ算の解き方です。簡単でしょう。
※最後の足し算を忘れることが多いので注意。
十の位が20以上になると、暗算しづらいものもある
今回は十の位が10のもの「14×13」を例として使ったので簡単に計算できましたが、20以上になると暗算での計算が難しくなっていきます。
- 図解1:「×20」や「×30」をする必要がでてくる
- 図解3:繰り上がりの足し算が出てくる場合があるので、暗算で計算しづらいものもある
暗算が難しくなるので、20以上の場合は少し練習が必要。
試しに「27✕26」をおみやげ算で計算してみると以下の計算になります。
- 「27✕26」→「33✕20=660」(←かける20を暗算でする必要がある)
- 「7×6=42」
- 「660+42=702」(←繰り上がりの足し算が出てくる)
1の部分の掛け算、3つ目の足し算の繰り上がりを少し練習をすれば、どの掛け算でも解くことができるので練習して見て下さい。
おみやげ算で計算した後は電卓で計算し、答えが同じであれば完璧です。
※ただし10の位が同じ数のみ
おみやげ算の証明
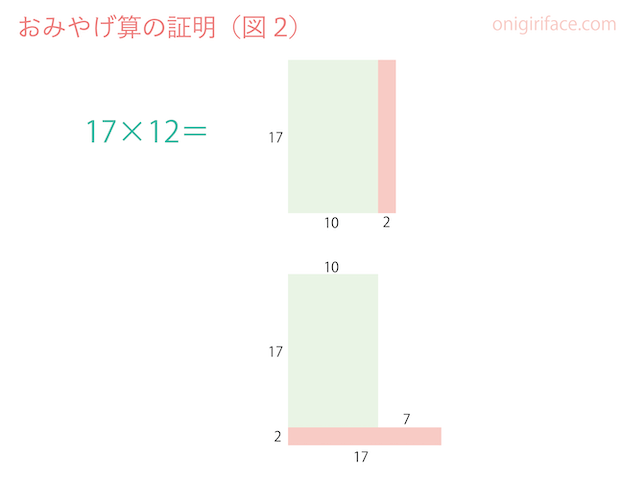
おみやげ算を使った計算は意外と簡単だったと思います。
「なぜそのようになるのか?」については上の「おみやげ算の証明(図2)」を見てもらうとイメージしやすくなります。
より詳しくは「おみやげ算をわかりやすく図で証明」で解説しているので見て下さい。
最後の足し算を忘れないように、この図(おみやげ算の証明:図2)を毎回イメージするようにしましょう。
最後に
おみやげ算が(イメージしていたよりも)簡単に計算できることがわかったかと思います。
まずは「11×11」から「19×19」からおみやげ算で計算してみて、暗算で解く練習に慣れるようにして下さい。
それを踏まえてから20以上、30以上の掛け算をおみやげ算で練習していきましょう。
インド式計算には種類があります。一覧とやり方をまとめています▼
関連:「インド式計算の達人」ホームページに戻る