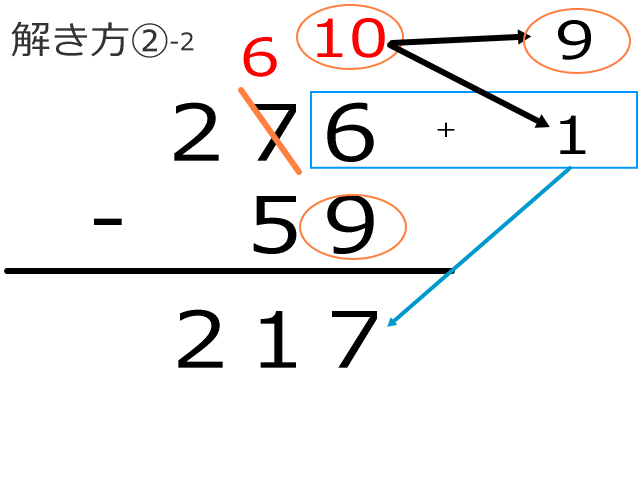
小学校低学年の算数で一番ややこしいのが繰り下がりの引き算です。
小学1年生では一つの筆算の中に繰り下がりが1回ですが、小学2年生では2回、小学3年生では3回出てきたりと難易度は少しずつ上っていきます。
現在、子供は小学3年生。
この3年間娘の算数を見てきて、繰り下がりの引き算には解き方・考え方が複数あることがわかりました。
そこで今回は繰り下がりの引き算の解き方を2パターン紹介します。
どちらの解き方も正しいのですが、子供の性格やその時の習得度によって使い分けできるかなと思います。
※記事の後半に「さくらんぼ計算・引き算」の練習問題プリントを追加したので、ぜひ活用して下さい。
繰り下がりの引き算の解き方・考え方1
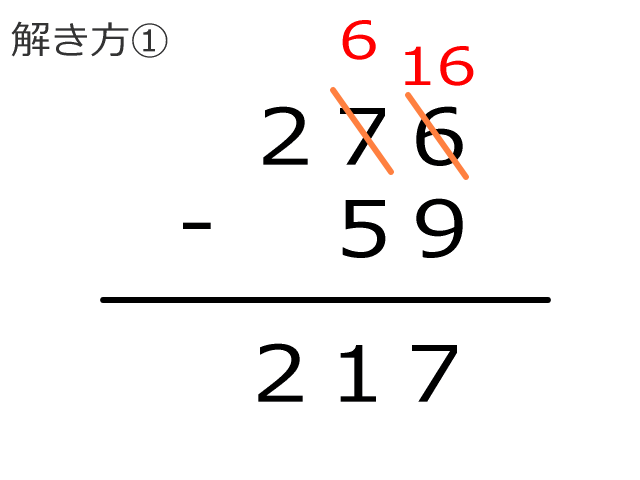
まずは1つ目の解き方です。上に例題(276-59)を用意しました。繰り下がりの数は考え方がわかるように1つだけにしています。
1の位は引き算できない場合、隣の10の位から10借りてきます。上の例題だと、10借りてきたので、10+6=16になりました。
その16から下の9を引くと、一の位は7となります。これがとてもシンプルな解き方です。
しかし、この16-9がすぐにできる子供とできない子供がいます。
そうなるとここでストップし、答えを間違う、または時間がかかりすぎて他の問題に進めないということが起こります。
小1や小2の場合、これが苦手な子供も多いでしょう。うちの子供はまさにそれでした。
もし解けない場合は次の解き方2を見て下さい。
繰り下がりの引き算の解き方・考え方2−1
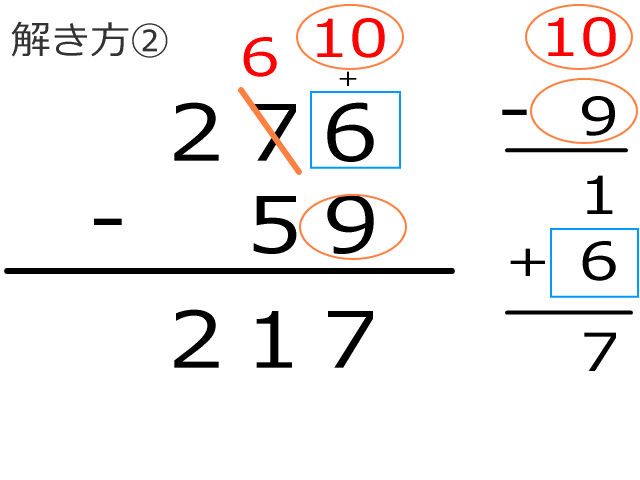
次に2つ目の解き方です。先ほどと同じ例題「276-59」で進めます。
1の位、6から9が引けないので、10の位から10を借りてきます。ここまでは同じです。
この借りてきた10から1の位の下にある9を引きます。すると答えは1になります(上の図のオレンジ色の楕円参照)。
その答えの1と上の6(図の青色の四角)と足すと、一の位は7となります。
図の右側にある筆算がこの解き方です。
もう少しわかりやすく書くと、隣りから借りてきた10から先に下の数字を引いて、その答えと上の数字を足すという考え方です。
繰り下がりの引き算の解き方・考え方2−2(さくらんぼ計算)
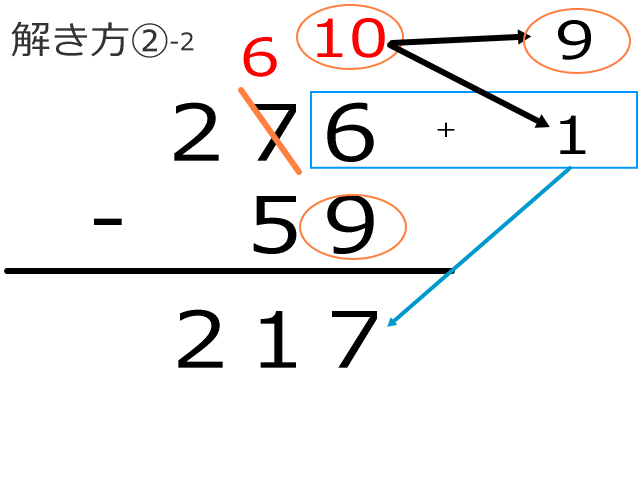
先程の解き方2と似た考え方を別の図で紹介します。
繰り下がりの場合、借りてくる数字は必ず10になります。その10から1の位の下の数字(ここでは9)を見ます。
見てすぐに「10は9と1」というさくらんぼ計算をします。
これができればすぐに1が出るので、最後に1の位の上の数字(ここでは6)を足せば、一の位は7となるわけです。
さくらんぼ計算については、小学1年生の教科書の初期に出てくるのでかなりの違和感があるのですが、こういう場面で役に立ちます。
繰り下がりの場合、必ず10を借りてくるということを念頭に置くと、10は1と何?を繰り返し頭で練習するのが良いかと思います。
- 10は1と9
- 10は2と8
- 10は3と7
- 10は4と6
- 10は5と5
- 10は6と4
- 10は7と3
- 10は8と2
- 10は9と1
これをお風呂の時でもいいので、小学1年生や2年生の時に繰り返して練習しておくと、解き方2-2はイメージしやすくなると思います。
以上の教え方は「さくらんぼ計算・引き算」の応用になります。この解き方の方が応用がききやすいかなと思います。
さらに詳しく
別サイト「おうち学習キッズ」に「さくらんぼ計算・繰り下がりのある引き算(2桁-1桁)」の練習プリントを作りました。
この問題を何度も解くことで、繰り下がりの引き算に慣れてくると思います。ぜひ活用してみて下さいね。
いくつといくつ表・ポスター「10はいくつといくつ」を部屋に貼っておくこともおすすめです。
まとめ

繰り下がりの引き座の解き方・考え方をまとめます。
- 解き方1:借りてきた10を足して16-9=7で解く
- 解き方2:借りてきた10から先に下の数字を引き、その答えと上の数字を足す(さくらんぼ計算・引き算)
大人になると「解き方2」の方を無意識にしています。一般的な考え方だとこの方が良いかと思います。
「解き方1」だと16-9や15-7などがすぐに解けないと難易度は高くなります。
小学生の子供をこの3年間見てきて、あまりにも繰り下がりの引き算が苦手なので、ある日を境に教え方を「解き方2」に変更しました。
すぐにできる子供ならこれはスーッと理解していくと思います。
しかしうちの子供の場合は「先に下を引いて、そして上を足す」ということが難しいのです。ゴチャゴチャになるみたいですね。
何度も何度も丁寧に説明しましたが理解できません。どうやら現況では理解できる能力に達していないことがわかりました。
親はこの件で悩みつつもそのまま月日が経ち小学3年生になりました。
するとどうでしょう、「解き方1」の16-9などが突然解けるようになっていたのです。
これにはビックリしました。
その時にわかったことは、小学校の勉強はついていけなくなると焦りますが、暫く現状維持で行くと、ある日を境に急に理解しているときがやってくるということです(全てではありませんが)。
これと似た場面を何度か見てきたので「今できないからもうダメだ」と諦めないで、気長に嫌いにならない程度に続けていけば良いのかなと考え方に変わりました。
極端に言うと、もし算数の解き方がわからなければ、今は答えだけを教えても良いのかなと。
そして学年が変わった時など、子供の脳が発達した時に急に理解している時がやってくるので、今理解できないのなら、小学6年生までに理解できればいいかなというぐらいの気持ちで最近は気楽に教えています。
